Como maestro de kindergarten, recibí atisbos de mi futuro cada febrero durante la inscripción al kindergarten. Mientras otros miembros del personal de la escuela ayudaban a los padres a llenar formularios, yo realizaba el examen, ordenado por el estado, de quienes pronto serían mis estudiantes, muchos de ellos aún asombrados niños de 4 años, más acostumbrados a los juegos simbólicos que a las evaluaciones formales. Durante el examen, les pedía que identificaran y describieran diversos objetos (un balón, un botón, un auto), que se pararan en un pie, que brincaran por el pasillo, que dibujaran una persona y que copiaran cuatro formas simples. La mayoría de los niños creían que solo estábamos jugando, pero algunos me miraban perplejos, como si quisieran decir: “¿Qué clase de maestro no sabe lo que es un botón?”. Sinceramente, yo coincidía con los niños que se desconcertaban; el examen me resultaba tan extraño y fuera de contexto a mí como les resultaba a ellos.

La mayoría de las veces, yo calcularía el puntaje del niño, notaría que supera el mínimo de corte y archivaría la hoja de registro en una carpeta de la que nunca saldría. Yo valoraba el examen del kindergarten ya que la interacción personal e individual me permitía hacerme una idea de cómo serían mis futuros alumnos, pero los resultados de las evaluaciones rara vez me interesaban.

¿Por qué debería importarme si un niño pequeño es capaz de copiar un cuadrado? ¿Qué podría presagiar una tarea tan trivial? Ahora, después de haber analizado la investigación, veo que copiar diseños es una competencia esencial con fuertes implicancias en cuanto a cómo cultivamos el conocimiento y las habilidades de los niños pequeños en lo que se refiere a las matemáticas.

—Tony Byers

En efecto, todos podríamos preguntarnos qué relación tiene la capacidad de una niña para copiar un cuadrado con el desarrollo de sus destrezas matemáticas. Sin embargo, la investigación indica que se puede predecir el futuro desempeño de un niño de 4 años en las matemáticas al observar cuán bien puede copiar una forma relativamente simple. Esta competencia, conocida entre los investigadores como copiar diseños, suele evaluarse en los niños pequeños como una de muchas maneras de medir la motricidad fina. Por ejemplo, en un conjunto de datos representativo a nivel nacional denominado Estudio Longitudinal sobre la Primera Infancia en el Kindergarten (Early Childhood Longitudinal Study of Kindergarten, ECLS-K), la propuesta de motricidad fina comprende tres tareas: construir un puente con bloques, dibujar una persona y copiar cinco diseños. Los estudios con este conjunto de datos indican que las competencias de motricidad fina que se miden durante el kindergarten predicen de manera contundente los logros matemáticos en primer, tercer y quinto grado, y que las competencias de motricidad fina pueden predecir tan bien los futuros logros académicos como las calificaciones de la atención de los niños que efectúan los maestros (Grissmer et al. 2010; Murrah 2010). Otro estudio sugiere que esta relación entre el desarrollo cognitivo y el desarrollo motriz podría tener lugar incluso antes de que los niños ingresen al kindergarten (Chen 2010). En conjuntos de datos que permiten análisis separados de las diferentes tareas de motricidad fina, copiar diseños suele ser la que mejor predice los futuros logros matemáticos en comparación con otros tipos de competencias de motricidad fina (Cameron et al. 2012; Carlson, Rowe y Curby 2013).

Competencias esenciales

¿Qué relación podría tener la representación temblorosa de una forma simple realizada por un niño de 4 años con las matemáticas? La forma más fácil de analizar esta conexión es aumentar la dificultad de la tarea al nivel de competencia de un adulto. Si bien la mayoría de los adultos puede copiar fácilmente un cuadrado, ¿cuántos pueden hacer lo mismo con una figura más compleja, como un dodecaedro? La mayoría de los adultos tiene las competencias de motricidad fina necesarias para completar el desafío, pero algo más determina si producimos un dodecaedro bonito y nítido, o dibujamos un balón de fútbol desinflado. Intente copiar el dodecaedro que se muestra. Es probable que usted comience a fragmentar mentalmente la figura en partes, a cambiar la atención entre el modelo y el dibujo, a luchar por trasladar a la página su imagen mental de la figura, a controlar el progreso y a corregir los errores.

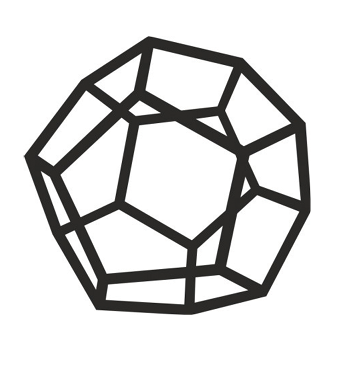
Las tareas de copiado pueden resultar difíciles tanto para los niños como para los adultos, ya que dependen de una amplia gama de competencias espaciales, por ejemplo, ensamblar las partes de un conjunto, comprender las relaciones espaciales y visualizar objetos desde varias perspectivas (Uttal et al. 2013; Verdine et al. 2014). Nuestra capacidad espacial no solo nos permite comprender lo que vemos y explorar el mundo; también está conectada con nuestra capacidad de hacer cálculos matemáticos. Un corpus de investigaciones considerable muestra superposiciones entre las áreas del cerebro que procesan información espacial y aquellas que procesan información numérica, como la ubicación y el tamaño (para consultar un análisis técnico interesante, véase el capítulo 10 de Dehaene 2011). Las áreas del cerebro que evolucionaron para encargarse de la numeralidad básica (como el sentido numérico) reclutan a las áreas cercanas orientadas hacia lo espacial para que las ayuden con las operaciones matemáticas más complicadas (como la aritmética simple). En consecuencia, las competencias espaciales están relacionadas con la capacidad para las matemáticas en general (Bull, Espy y Wiebe 2008) y a menudo se ven afectadas en las personas con dificultades de aprendizaje de las matemáticas (Geary 2013). Además, los alumnos de secundaria que obtienen buenos resultados en las pruebas de competencias espaciales tienen más probabilidades de seguir carreras de ciencia, tecnología, ingeniería y matemáticas (CTIM) que sus pares con calificaciones más bajas (Wai, Lubinski y Benbow 2009).

Las actividades que apoyan los logros matemáticos no siempre se parecen a las matemáticas.

Por supuesto, las competencias espaciales no son las únicas responsables de que un niño pueda copiar bien un diseño. Las tareas de copiado de diseños también requieren una función ejecutiva, un término que resulta cada vez más familiar para los docentes de educación inicial. La función ejecutiva abarca un conjunto de distintas competencias que incluyen: mantener la atención, cambiar la atención de manera deliberada, controlar impulsos, y retener información y procedimientos en la memoria operativa (Best y Miller 2010). Concretamente, estas son competencias cognitivas que permiten a los niños controlar su razonamiento y comportamiento (McClelland y Cameron 2012). Es posible que los niños que tienen problemas para guardar sus pertenencias en sus cubículos, que vagan de una actividad a otra y que no parecen recordar instrucciones simples de varios pasos presenten dificultades con uno o más componentes de la función ejecutiva.

Tanto el copiado de diseños como las matemáticas plantean exigencias similares para la función ejecutiva. Al copiar, el niño debe planificar el orden en el cual replicará las partes del diseño, y mantener una representación del diseño y de su planificación en su memoria operativa mientras cambia su atención del modelo al dibujo. Al realizar cálculos matemáticos, las exigencias son similares y la función ejecutiva se asocia sistemáticamente con el desempeño en matemáticas, particularmente durante los primeros años de la escuela primaria (McClelland y Cameron 2012; Verdine et al. 2014).

La función ejecutiva y las competencias espaciales se abren paso en las aulas del kindergarten en múltiples formas, en especial durante la enseñanza de las matemáticas. En el sector de kindergarten 2 de la mayoría de las escuelas primarias, los trabajos de los niños que se exhiben normalmente se basan en gran medida en la función ejecutiva, y en las habilidades espaciales para planificar y crear. En la imagen, se muestra un ejemplo de una de esas creaciones expuesta en el exterior de un aula de kindergarten en Charlottesville, Virginia, Estados Unidos. En esta lección, el maestro ayudó a los alumnos a que hicieran lo siguiente:

1. Pensar de manera discriminada acerca de la pregunta: “¿Puedes hacer una burbuja?” y separar la información superflua de la pertinente (dirigir la atención y controlar los impulsos)

2. Identificar en qué columna ubicar los círculos que representaban sus opiniones (memoria operativa y competencias espaciales)

3. Dibujar o pegar cada círculo en el papel de carnicero con el orden y el espaciado correctos (coordinación motora fina y competencias espaciales)

4. Responder preguntas en las que debían elaborar una conclusión, como: “¿Tu maestro puede hacer una burbuja?” y: “¿Cuál es más grande, la cantidad de niños que pueden hacer una burbuja o la cantidad de niños que no pueden?”, lo que se podía deducir mirando el gráfico (memoria operativa, cambio de atención, procesamiento de información espacial)

Al observar las lecciones de matemáticas a través de esta lente, es fácil darse cuenta por qué los niños con una función ejecutiva y competencias espaciales fuertemente desarrolladas adquieren la capacidad para las matemáticas con más facilidad que sus pares con mayores dificultades en esas áreas.

El copiado de diseños y las matemáticas requieren una combinación similar de competencias cognitivas, incluidas la función ejecutiva y las competencias espaciales.

Entonces, las tareas de copiado de diseños y las matemáticas están vinculadas porque ambas requieren una combinación similar de competencias cognitivas complejas e interrelacionadas, incluidas la función ejecutiva y las competencias espaciales. Para los maestros, conocer esto puede abrirles las puertas a una nueva clase de enseñanza de las matemáticas, una que no parece enfocarse en las matemáticas en lo absoluto.

De la teoría a la práctica

Concretamente, ¿cómo se pueden aplicar estos conocimientos a la enseñanza en las aulas? De la misma manera que practicar velocidad en la pista ayuda a un jugador de fútbol americano en el campo de juego, las competencias cognitivas que se perfeccionan durante las tareas de copiado de diseños pueden ayudar a los niños a aprender matemáticas. Sin embargo, los docentes de educación inicial pueden plantear una objeción razonable. Incluso el término copiado de diseños da la impresión de que se trata de un trabajo tedioso. Copiar cientos de diseños se asemeja al tipo de actividad inapropiada desde el punto de vista del desarrollo que no suele ser bienvenida en las aulas de preescolares y kindergarten de todo el país. ¿O quizás sí?

Analice las manualidades y los juegos que todos conocemos, que fueron la base de los preescolares, los campamentos, los programas extracurriculares y las tardes ociosas de domingo durante décadas. Materiales como Play-Doh, LEGO, lana, Colorforms, mostacillas fundibles y Wikki Stix ofrecen incontables horas de juego creativo, y también les da la posibilidad de recrear modelos con precisión, a veces trasladando imágenes en dos dimensiones a creaciones en tres dimensiones. ¿Qué hacen los niños cuando ensamblan cientos de pequeñas piezas de LEGO para formar el barco pirata que ven en el frente de la caja si no es copiar un diseño? Un equipo de investigadores, docentes y psicólogos (incluidos los autores de este artículo) utilizó estos conocimientos para crear y probar un currículo que tiene por objeto mejorar las competencias básicas de matemáticas mediante actividades divertidas de copiado de diseños.

Minds in Motion (Mentes en movimiento)

En un aula de actividades extracurriculares, siete niños de kindergarten típicamente bulliciosos se inclinan sobre sus diseños de mostacillas fundidas mientras ubican cuidadosamente pequeñas mostacillas en sus aún más pequeños lugares. Intentan copiar los diseños que su maestro adaptó a sus niveles de competencia. Toman varias mostacillas a la vez, las cuentan y las eligen, y las acomodan para que coincidan con sus modelos. A medida que trabajan, su instructor controla su progreso y les brinda pistas verbales, a menudo cargadas de un lenguaje espacial, como: “¿La mostacilla amarilla va arriba o abajo de la mostacilla anaranjada?”

Este tipo de actividad focalizada de manualidades y arte, conocida por muchos docentes de educación inicial, es la esencia del currículo de Minds in Motion (Brock et al. 2017). Minds in Motion está diseñado para complementar y mejorar el desarrollo motriz y cognitivo entre los 4 y los 7 años. Cada lección capitaliza los hitos del desarrollo, como la capacidad de copiar formas geométricas o letras de imprenta, apilar 10 bloques o más, reconocer al menos cuatro colores y seguir instrucciones de dos o tres pasos (Academia Estadounidense de Pediatría 2009) A fin de respetar la variabilidad en el desarrollo de los niños, el programa no solo diferencia los procesos mediante los cuales los niños completan las tareas, sino también los diseños específicos que copian.

Minds in Motion utiliza materiales y realiza actividades que están fácilmente disponibles en la mayoría de las aulas de preescolares y kindergarten, por lo que es razonable pensar que los niños ya están perfeccionando su función ejecutiva y sus competencias espaciales cuando utilizan los materiales de una forma menos estructurada (para obtener un análisis del razonamiento espacial y cómo incorporarlo a todo el currículo, consulte Newcombe y Frick 2010). Sin embargo, muchos niños, especialmente aquellos que provienen de familias con recursos limitados que probablemente no hayan tenido muchas oportunidades de jugar con materiales como LEGO o Play-Doh, tienden a ingresar al kindergarten con una función ejecutiva y competencias espaciales menos desarrolladas que las de sus pares (Levine et al. 2012; Potter, Mashburn y Grissmer 2013). Es posible que estos alumnos se beneficien con las actividades de copiado de diseño más estructuradas, que entran en la categoría de juego guiado con objetos, junto con experiencias de exploración menos estructuradas (Weisberg, Hirsh-Pasek y Golinkoff 2013; Cameron et al., próximamente). Los resultados de un estudio realizado a Minds in Motion proporcionan evidencia convincente de que las actividades de copiado de diseños estructuradas pueden mejorar la función ejecutiva y las competencias espaciales de los niños que viven en la pobreza (Brock et al. 2017); los análisis realizados por el equipo de investigación también sugieren que estas actividades tienen el potencial de mejorar las calificaciones en matemáticas (Grissmer et al. 2013).

Aunque Minds in Motion actualmente solo está disponible para maestros que participan de una evaluación del programa, los principios fundamentales del currículo pueden incorporarse con poca preparación en la mayoría de las aulas de educación inicial. Normalmente, los maestros tienen a mano muchos de los materiales que se necesitan para copiar diseños (como crayones, trozos de fieltro, bloques y mostacillas), por lo que lo único que deberían agregar son modelos creativos y coloridos para copiar. Comience con modelos relativamente simples y continúe con otros más complejos a medida que los niños adquieran mayor capacidad. Evalúe dedicar un centro al copiado de diseños, y alterne materiales y modelos interesantes en él. Y utilice y fomente el vocabulario espacial, como arriba, abajo, al lado, en el medio y girar, a medida que les explica a los niños cada tarea y los guía para completarla; ese lenguaje ayuda a los niños a desarrollar un razonamiento espacial, especialmente si los niños también utilizan esos términos (Pruden, Levine y Huttenlocher 2011).

Conclusión

El copiado de diseños puede mejorar la capacidad de los alumnos para las matemáticas, pero el mensaje más importante para los maestros no es que deben hacer que sus alumnos copien diseños, sino que las actividades que apoyan el rendimiento matemático no siempre se parecen a las matemáticas. El copiado de diseños ejercita y desarrolla las competencias cognitivas subyacentes, principalmente la función ejecutiva y las competencias espaciales, que contribuyen a la capacidad para las matemáticas. Estas competencias cognitivas proporcionan los cimientos para el aprendizaje posterior en otras materias también. Pero no es una idea nueva. Friedrich Froebel, el inventor del kindergarten, basó su currículo en torno a ofrecerles a los niños una serie de supuestos obsequios, muchos de los cuales son materiales de construcción para utilizar en actividades bastante similares al copiado de diseños. Los ecos de los métodos de Froebel están presentes en cada centro de bloques y en cada balde de bloques para formar diseños. Las investigaciones psicológicas y sobre educación modernas sugieren que es posible que la intuición de Froebel de alentar a los niños pequeños a observar, tocar y crear haya sido correcta, al menos en lo que respecta a la enseñanza de las matemáticas. En palabras de uno de los biógrafos de Froebel, el “reconocimiento y la valoración de la forma antes que la nomenclatura” era evidente para él y actualmente es igual de evidente para los profesionales de la educación inicial (Brosterman 1997, 22).

Referencias

American Academy of Pediatrics. 2009. Caring for Your Baby and Young Child: Birth to Age 5. 5th ed. New York: Bantam.

Best, J.R., & P.H. Miller. 2010. “A Developmental Perspective on Executive Function.” Child Development 81 (6): 1641–60.

Brock, L.L., W.M. Murrah, E.A. Cottone, A.J. Mashburn, & D.W. Grissmer. 2017. “An Afterschool Intervention Targeting Executive Function and Visuospatial Skills Also Improves Classroom Behavior.” International Journal of Behavioral Development.

Brosterman, N. 1997. Inventing Kindergarten. New York: Harry N. Abrams.

Bull, R., K.A. Espy, & S.A. Wiebe. 2008. “Short-Term Memory, Working Memory, and Executive Functioning in Preschoolers: Longitudinal Predictors of Mathematical Achievement at Age 7 Years.” Developmental Neuropsychology 33 (3): 205–28.

Cameron, C.E., L.L. Brock, W.M. Murrah, L.H. Bell, S.L. Worzalla, D.W. Grissmer, & F.J. Morrison. 2012. “Fine Motor Skills and Executive Function Both Contribute to Kindergarten Achievement.” Child Development 83 (4): 1229–44.

Cameron, C.E., L.L. Brock, W.M. Murrah, L.H. Bell, S.L. Worzalla, D.W. Grissmer, & F.J. Morrison. Forthcoming. Hands-On, Minds on: How Executive Function, Motor, and Spatial Skills Foster School Readiness. New York: Teachers College Press.

Carlson, A.G., E. Rowe, & T.W. Curby. 2013. “Disentangling Fine Motor Skills’ Relations to Academic Achievement: The Relative Contributions of Visual-Spatial Integration and Visual-Motor Coordination.” Journal of Genetic Psychology 174 (5–6): 514–33.

Chen, W.-B. 2010. “Fine Motor Skills As a Mediator of the Relationship between Parent-Child Interaction Quality and Child Cognitive Ability.” PhD dissertation, University of Virginia.

Dehaene, S. 2011. “The Number Sense: Fifteen Years Later.” Chap. 10 in The Number Sense: How the Mind Creates Mathematics. Rev. ed. New York: Oxford University Press.

Geary, D.C. 2013. “Early Foundations for Mathematics Learning and Their Relations to Learning Disabilities.” Current Directions in Psychological Science 22 (1): 23–27.

Grissmer, D.W., K.J. Grimm, S.M. Aiyer, W.M. Murrah, & J.S. Steele. 2010. “Fine Motor Skills and Early Comprehension of the World: Two New School Readiness Indicators.” Developmental Psychology 46 (5): 1008–17.

Grissmer, D.W., A. Mashburn, E. Cottone, L.L. Brock, W.M. Murrah, J. Blodgett, & C.E. Cameron. 2013. The Efficacy of Minds in Motion on Children’s Development of Executive Function, Visuo-Spatial and Math Skills. Paper presented at the Society for Research on Educational Effectiveness (SREE), Washington, DC. www.sree.org/conferences/2013f/program/downloads/abstracts/1003_4.pdf.

Levine, S.C., K.R. Ratliff, J. Huttenlocher, & J. Cannon. 2012. “Early Puzzle Play: A Predictor of Preschoolers’ Spatial Transformation Skill.” Developmental Psychology 48 (2): 530–42.

McClelland, M.M., & C.E. Cameron. 2012. “Self-Regulation in Early Childhood: Improving Conceptual Clarity and Developing Ecologically Valid Measures.” Child Development Perspectives 6 (2): 136–42.

Murrah, W.M. 2010. “Comparing Self-Regulatory and Early Academic Skills As Predictors of Later Math, Reading, and Science Elementary School Achievement.” Doctoral dissertation, University of Virginia..

Newcombe, N.S., & A. Frick. 2010. “Early Education for Spatial Intelligence: Why, What, and How.” Mind, Brain and Education 4 (3): 102–11.

Potter, D., A. Mashburn, & D.W. Grissmer. 2013. “The Family, Neuroscience, and Academic Skills: An Interdisciplinary Account of Social Class Gaps in Children’s Test Scores.” Social Science Research 42 (2): 446–64.

Pruden, S.M., S.C. Levine, & J. Huttenlocher. 2011. “Children’s Spatial Thinking: Does Talk about the Spatial World Matter?” Developmental Science 14 (6): 1417–30.

Uttal, D.H., N.G. Meadow, E. Tipton, L.L. Hand, A.R. Alden, C. Warren, & N.S. Newcombe. 2013. “The Malleability of Spatial Skills: A Meta-Analysis of Training Studies.” Psychological Bulletin 139 (2): 352–402.

Verdine, B.N., C.M. Irwin, R.M. Golinkoff, & K. Hirsh-Pasek 2014. “Contributions of Executive Function and Spatial Skills to Preschool Mathematics Achievement.” Journal of Experimental Child Psychology 126: 37–51.

Wai, J., D. Lubinski, & C.P. Benbow. 2009. “Spatial Ability for STEM Domains: Aligning over 50 Years of Cumulative Psychological Knowledge Solidifies Its Importance.” Journal of Educational Psychology 101 (4): 817–35.

Weisberg, D., K. Hirsh-Pasek, & R.M. Golinkoff. 2013. “Guided Play: Where Curricular Goals Meet a Playful Pedagogy.” Mind, Brain, and Education 7 (2): 104–12.

Photographs: © Getty Images; courtesy of the author