Most teachers can observe Tina’s mathematical abilities. Less apparent, perhaps, is her growing proficiency in using executive function to grapple with complicated tasks. Tina is holding multiple pieces of information in her mind, which help her conclude that she is feeling a triangle. She is sustaining her attention and regulating her physical actions as she engages in this task. She cognitively shifts from thinking about the properties of the shape to the name of the shape. As Tina improves her understanding of math, she is simultaneously developing the higher-order mental skills and abilities that will help her complete tasks like the feely box activity. Similarly, the young children around her are inhibiting impulses and regulating their behaviors as they wait their turn. All of these skills serve as the behind-the-scenes machinery that facilitates young children’s ability to engage in and demonstrate their mathematical competency.

The Role of Executive Function

Executive function consists of the processes involved in regulating impulses, attention, behavior, planning, and thinking. The concept is complex, and research continues to help us better understand and assess its contributions to learning and development over time. Still, one clear and consistent finding is that executive function is predictive of early academic outcomes and influences a range of developmental areas during early childhood (Nesbitt, Farran, & Dong 2014; Ackerman & Friedman-Krauss 2017; Fuhs et al. 2017; Pascual, Munoz, & Robres 2019). These include physical, social and emotional, and cognitive domains. The need for executive function in math learning is especially well-established (Cragg & Gilmore 2014; Clements, Sarama, & Germeroth 2016).

Three processes are usually described as key components of executive function, all of which are foundational for learning:

• Cognitive flexibility involves the ability to switch one’s attention to different aspects of a problem or to approach a problem using a variety of strategies. For instance, a preschooler asked to iteratively sort objects according to different characteristics, such as size, shape, and color, is using cognitive flexibility.
• Working memory is the maintenance, updating, and integrating of incoming information. A teacher may, for example, show a 4-year-old that she has four books and receives one more. The 4-year-old must cognitively maintain the starting number (4) and update it by one to arrive at the new total (5).
• Inhibitory control refers to the regulation of impulsive behaviors, such as talking over the teacher, and the suppression of automatic responses, such as calling all quadrilaterals “squares.” Inhibitory control can be both behavioral and cognitive:
  • Behavioral inhibitory control refers to orienting one’s physical actions and body to support the completion of a task. A child who stays seated to draw a picture rather than jumping out of the chair repeatedly and not finishing the drawing exhibits behavioral inhibitory control.
  • Cognitive inhibitory control refers to mental actions that support the completion of a task, such as sustaining attention and suppressing automatic responses. A child who carefully observes the differences between a square and a rectangle rather than calling them both squares is exhibiting cognitive inhibitory control.

Both types of inhibitory control are highly interrelated and can often be difficult to distinguish from one another.

No one is born with fully developed executive function skills; rather, we are born with the potential to develop them (Blair 2016). This requires intentional and ongoing teacher support (Center on the Developing Child 2012). In this article, we use a geometry activity called “What Shape Am I Touching?” (below) as a context for understanding how various executive function processes can be applied and supported during a math lesson. We then provide broader takeaways for supporting executive function that preschool and prekindergarten teachers can use across content areas.

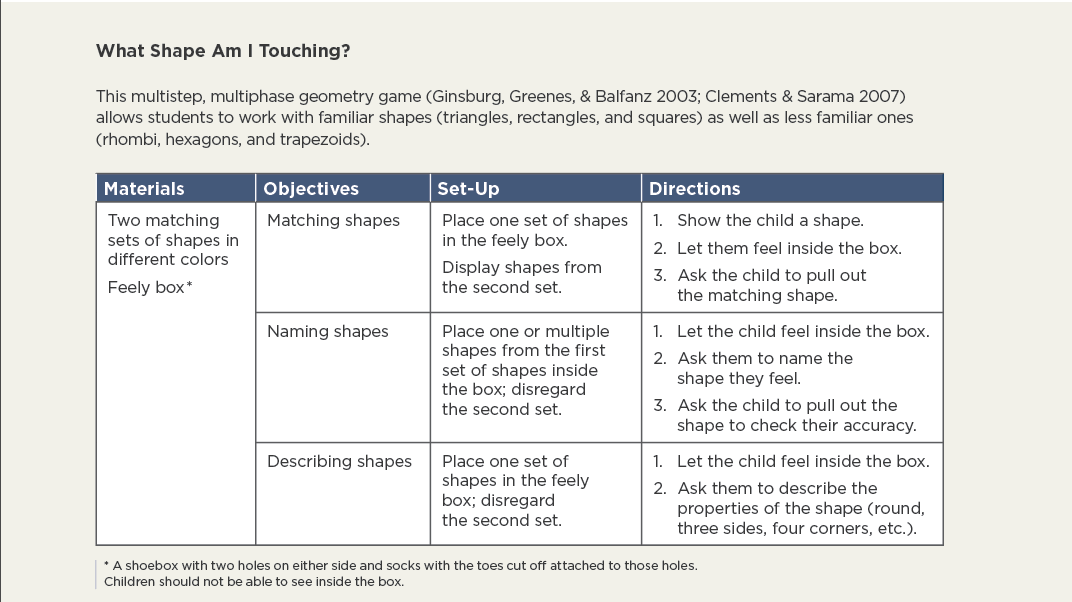
Geometry as a Context for Executive Function Development

“What Shape Am I Touching?” stems from the Development and Research in Early Mathematics Education (DREME) Network. As a group of researchers from 12 different universities, DREME spent over five years exploring multiple topics related to young children’s early math learning, including relations between early math and executive function competencies. In our work with the network, we used “What Shape Am I Touching?” because of its two key attributes: it is an engaging, multimodal activity that fosters early mathematics learning, and it is an example of an activity that creates ample space for children to tap into their developing executive function skills. Children must mentally hold and integrate multiple pieces of information; shift between different types of tasks as they match, name, and describe shapes; wait their turn and control their impulses; and focus their attention. By examining “What Shape Am I Touching?” and the teacher-child interactions during it, we will explore all three executive function processes—cognitive flexibility, working memory, and inhibitory control—and illustrate how the teachers supported preschoolers’ developing executive function as they played.

Cognitive Flexibility

In the above vignette, a subtle shift occurs. Andrea holds up a rhombus for Sabala to match and also asks Sabala to name the four-sided shape. Sabala thus moves from one facet of understanding shapes (matching shapes based on feeling their properties) to another (recalling shape names). This requires her to transfer her attention among multiple aspects of the problem (understanding what a rhombus is and why). It is important to note that

• Teacher prompting elicited cognitive flexibility. Alexis asked Sabala to match and then to name the shape.
• Teacher prompting can be planned ahead of time or be spontaneous. Teachers and others may think they have to create intricate or elaborate tasks. In reality, intentionally planned activities that rely on simple steps and inexpensive materials can effectively exercise children’s cognitive flexibility.

Working Memory

Here, Alexis supports Julie’s working memory in two ways:

• Alexis creates challenges to spur working memory. Julie must recall multiple steps during this activity. She has to identify shapes by feel, remember not to look inside the box, refrain from pulling out the shape (unless she has matched or already identified it), and trade turns with a partner. Regardless of children’s mathematical accuracy when playing this game, remembering and following these steps will cultivate and expand preschoolers’ abilities to maintain multiple pieces of information.
• Alexis presents problems that require children not only to maintain but also to update multiple pieces of information. In order to name the shape, Julie has to consider what she is feeling and then integrate that information to determine what she is touching in the feely box.

Children do not need to have progressed to identifying sides versus vertices to improve their working memories. (See “Vertices, Angles, and Corners: Teaching Shapes to Preschoolers” below.) Alexis could ask more open-ended questions, such as, “Tell me two things you feel about this shape. What shape do you think it is? Why do you think that?” As long as children are holding and integrating more than one piece of information, they are practicing using their working memories.

Inhibitory Control

Without intentional preparation and support, novel materials can be distracting—feely boxes can rapidly transform into oversized maracas. However, with thoughtful planning and guidance, “What Shape Am I Touching?” gives children an opportunity to practice inhibiting impulsive behaviors. For example, the teachers we worked with often introduced the game with a hand on the box to help children avoid shaking or throwing it. As children demonstrated that they could use the materials appropriately, teachers gave them more choice and control.

In the case of Darci, two types of inhibitory control are on display—both behavioral and cognitive. Behaviorally, she does not peek inside the box but instead closes her eyes to focus on feeling and matching shapes. More broadly, both she and Virginia use the feely box and shape sets with care, focus, and fairness.

With regard to cognitive inhibitory control, Darci faces an elegant challenge. She has to suppress the automatic response to pull out the first rectangle she feels and instead attend to the shape’s properties as well as the size of those properties. (Are the sides longer or shorter? Does the rectangle feel long and skinny or not?) She potentially must compare the three rectangles to each another before settling on her choice for the match.

Engaging Executive Function Throughout the Day

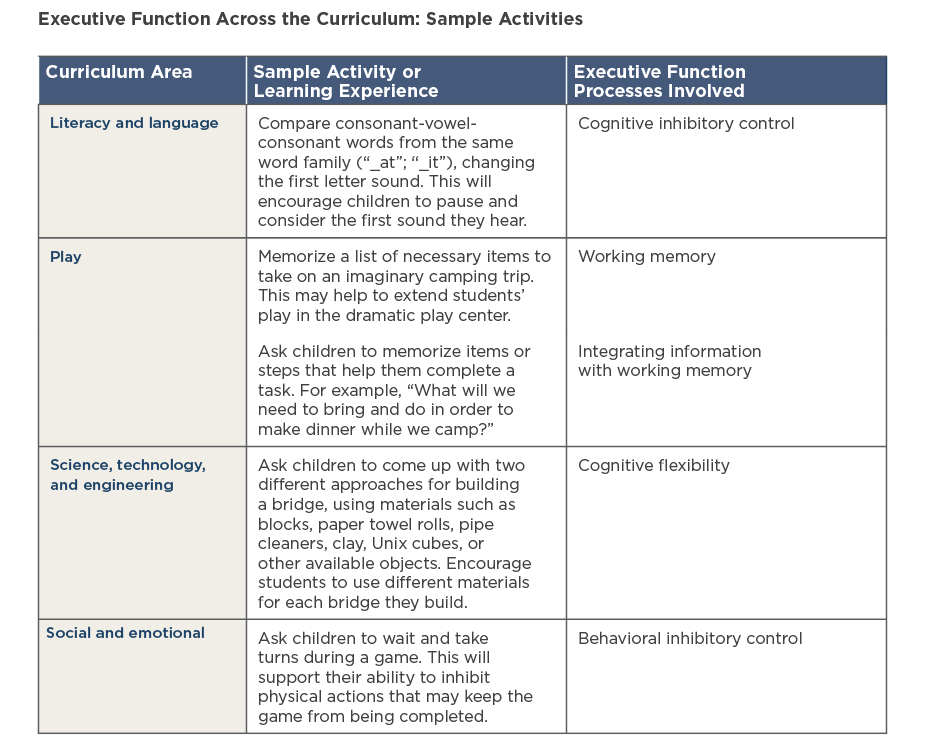
Developing executive function is most meaningful when integrated into other daily content—trying to provide separate “executive function lessons” can be too abstract for young children to grasp. In this article, we presented one geometry game that encourages the activation of three executive function processes through early mathematics learning. Early childhood educators can use it as a model to foster executive function across the curriculum and throughout the day. (See “Executive Function Across the Curriculum: Sample Activities” below for sample learning experiences.) Here are three strategies.

Create Opportunities for Cognitive Flexibility

Engaging cognitive flexibility is demanding for children of any age. Children often become comfortable approaching a problem with a single strategy or visualizing a problem using a set representation, even if that strategy or representation is inefficient. For example, children who become accustomed to sorting by color may struggle to begin sorting by shape or size, even if that method is more appropriate for the task at hand. Or, in the vignette above, Sabala may become so used to matching that she has difficulty when Alexis asks her to shift into naming shapes. Anticipating this, teachers can help children develop cognitive flexibility by embedding daily opportunities for them to see or solve problems in new ways.

Stretch Children’s Working Memories

A strong working memory requires regular practice. Ultimately, only consistent engagement in multistep activities and complex problems will help children learn how to use their working memories efficiently.

We observe that there are two mechanisms by which teachers can challenge preschoolers’ working memories:

• providing activities in which children must remember and follow through on multiple steps
• giving children problems that require them to maintain and update multiple pieces of information

Because preschool children’s working memories are still emerging, two or three pieces of information are sufficiently taxing for them. They also need significant support. For example, our teachers often prompted students about the properties of shapes, such as, “How does the shape feel? How many sides does it have? Are they straight sides?” Children acquired specific types of information through these questions, but the teaching and learning did not stop there. Teachers offered space for children to explore and determine the answers themselves. They also built on children’s foundational knowledge about shape properties to add complexity and depth. As a result, we observed children not only recalling this information independently but also applying it to other situations.

For example, at the start of “What Shape Am I Touching?” teachers would lay out selected shapes on the table and ask children to make observations about them. A teacher might put out a rhombus and a trapezoid and ask, “What do you see?” Children could note that both shapes had four sides or that the rhombus had sides of equal length while the trapezoid did not. This type of exploration supported their ability to maintain and update information during the game itself.

Similarly, teachers occasionally deviated from the game by placing multiple shapes inside the feely box, asking children to select a shape inside of the box and to name it or to describe what they felt. This gave children an opportunity to explore shapes in the feely box independently and to use their working memories in the process.

Fully Engage Children’s Cognitive and Behavioral Inhibitory Control

Almost any learning experience can be considered an opportunity for preschoolers to engage their behavioral inhibitory control. Waiting for turns, raising hands to speak, lining up for the bathroom, and different transitions are all part of daily schedules and routines. These moments require children to suppress impulsive behaviors (grabbing or mishandling materials) in favor of more appropriate responses.

Children need opportunities to practice behavioral inhibitory control. Games like “What Shape Am I Touching?” offer them the opportunity to work with a small number of highly engaging materials, which in itself can be challenging. Activities with too many engaging materials can create distractions, whereas activities with too few appealing materials can elicit boredom or disinterest. Finding a balance is key and gives children chances to practice behavioral inhibitory control, gradually growing in this area.

Children can also practice cognitive inhibitory control—or avoiding automatic responses—across content areas. Consider the teacher who asks her class what bears eat and hears children shouting, “Leaves!” because she just taught them about a deer’s diet. Teachers can help children practice cognitive inhibitory control by reminding them to pause and carefully consider their responses before calling out.   

Conclusion

Each of the principles discussed in this article works in tandem with the others to help children regulate and facilitate their thinking, problem solving, and decision making. They are almost never neatly distinct from one another: a learning experience that asks children to engage their working memories may also encourage inhibitory control, for example. Early childhood educators can intentionally plan how to strengthen each executive function process by identifying how children use different aspects of their executive function across activities. As with the “What Shape Am I Touching?” game, teachers can then promote executive function through playful learning throughout the preschool day.

Photographs: Courtesy of Crystal Day-Hess.

Copyright © 2021 by the National Association for the Education of Young Children. See Permissions and Reprints online at NAEYC.org/resources/permissions.

References

Ackerman, D.J., & A.H. Friedman-Krauss. 2017. “Preschoolers’ Executive Function: Importance, Contributors, Research Needs and Assessment Options.” Child Development 85: 103–113.

Blair, C. 2016. “Developmental Science and Executive Function.” Current Directions in Psychological Science 25 (1): 3–7.

Center on the Developing Child. 2012. Executive Function (InBrief). Retrieved from www.developingchild.harvard.edu.

Clements, D.H., J. Sarama, & C. Germeroth. 2016. “Learning Executive Function and Early Mathematics: Directions of Causal Relations.” Early Childhood Research Quarterly 36: 79–90.

Clements, D.H., & J. Sarama. 2007. Building Blocks Curriculum, Grade PreK. Columbus, OH: SRA.

Clements, D.H., & J. Sarama. 2009. Learning and Teaching Early Math: The Learning Trajectories Approach. New York: Routledge.

Cragg, L., & C. Gilmore. 2014. “Skills Underlying Mathematics: The Role of Executive Function in the Development of Mathematics Proficiency.” Trends in Neuroscience and Education 3 (2): 63–68.

Fuhs, M.W., K.T. Nesbitt, D.C. Farran, & N. Dong. 2014. “Longitudinal Associations Between Executive Functioning and Academic Skills Across Content Areas.” Developmental Psychology 50 (6): 1698–1709.

Ginsburg, H.P., C.E. Greenes, & R. Balfanz. 2003. Big Math for Little Kids: Pre-Kindergarten. New York: Pearson Learning Group.

Pascual, A.C., N.M. Munoz, & A.Q. Robres. 2019. “The Relationship Between Executive Functions and Academic Performance in Primary Education: Review and Meta-Analysis.” Frontiers in Psychology 10: 1582.